上一节介绍了PriorityQueue的原理,先来简单的回顾一下 PriorityQueue 的原理
以最大堆为例来介绍
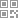
- PriorityQueue是用一棵完全二叉树实现的。
- 不但是棵完全二叉树,而且树中的每个根节点都比它的左右两个孩子节点元素大
- PriorityQueue底层是用数组来保存这棵完全二叉树的。
如下图,是一棵最大堆。 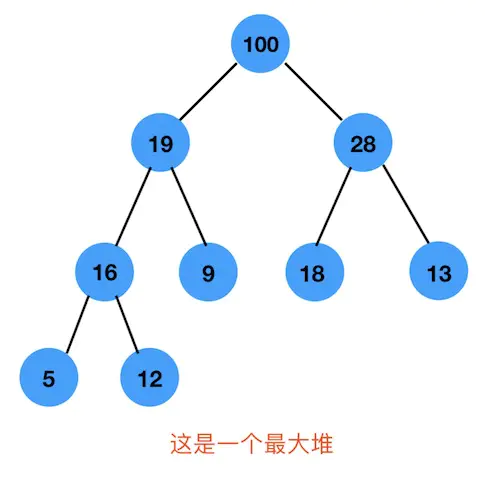
最大堆的删除操作 删除指的是删除根元素,也就是图中的100元素 删除元素也就是 shiftDown 操作,向下翻 删除一个根元素有以下步骤:
- 将100元素删除,将最后一个元素12放到100的位置上,12成为根节点
- 找出 12 这个节点的左右两个孩子节点中的最大的,也就是图中的28节点
- 12 出 28节点进行比较,如果12比28小,则交换位置
- 12节点继续重复2,3步骤,直到12比它的左右孩子节点都大则停止
最大堆插入一个节点 插入一个节点,也叫shiftUp操作,向上翻 以插入一个节点23为例,步骤如下:
- 将23放到二叉树的最后位置,也就是成为了9这个节点的左孩子
- 23与它的父节点进行比较,如果比它的父节点大,就交换位置
- 23这个节点继续重要第2步骤,直到比它的父节点小方停止比较
代码实现 首先我们先上两张图 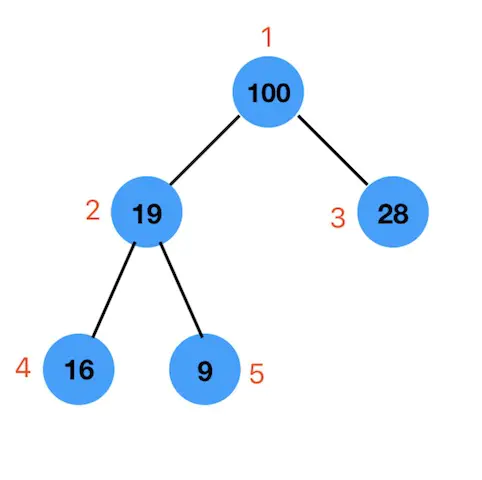
我们从左往右,按层序遍历,分别存放到数组的相应索引对应的位置上。 数组的第0个索引位置我们不用,从索引为1的位置开始存放。 最终这个最大堆存放到数组中,如下图 
首先实现一个最简单的只存 int 类型的优先级队列 QPriorityQueueInt 完整代码如下:
//最大堆,只存放int,并且没有扩容机制
public class QPriorityQueueInt {
//默认底层数据大小为10
private static int DEFAULT_INIT_CAPACITY = 10;
//底层数组
private int[] queue;
//节点的个数
private int size;
public QPriorityQueueInt() {
//因为数组是从索引 1 的位置开始存放,索引为 0 的位置不用
//所以开辟空间的时候需要加 1
queue = new int[DEFAULT_INIT_CAPACITY + 1];
//当前数组中节点的个数为0
size = 0;
}
//返回节点的个数
public int size() {
return size;
}
//最大堆是否为空
public boolean isEmpty() {
return size == 0;
}
//添加一个节点
public void add(int e) {
//将元素存放到数组当前最后一个位置上
queue[size + 1] = e;
//个数需要加1
size++;
//需要向上翻
shiftUp(size);
}
//向上翻,最大堆中的最后一个节点,不停的与父节点比较
//最大堆中父节点的索引是 k / 2
private void shiftUp(int k) {
// k > 1 ,说明从第2个节点开始,因为如果只有一个节点的话,不需要比较了
// queue[k] > queue[k / 2] ,当前节点大于父节点
while (k > 1 && queue[k] > queue[k / 2]) {
//交换位置
swap(k, k / 2);
//把父节点的索引赋值给 k,然后继续重复上面步骤
k = k / 2;
}
}
//删除最大堆中的节点
public int poll() {
//把第1个位置的节点保存起来
int result = queue[1];
//把最后一个节点放到第1个节点上面,成为整棵树的根节点
queue[1] = queue[size];
//别忘了size 要减1
size--;
//最后一个节点成为根节点后,就需要向下翻了
//向下翻的目的就是把大的节点翻上来
shiftDown(1);
//返回第1个节点,也就是队头节点
return result;
}
//向下翻
private void shiftDown(int k) {
//2 * k <= size ,2*k 是左孩子
//2 * k <= size ,是当前节点有左孩子
//至少有个左孩子才可以交换,因为是完全二叉树,左孩子没有,右孩子肯定没有
while (2 * k <= size) {
//比较左右两个孩子节点,将大的节点的索引赋值给 j
//左孩子索引
int j = 2 * k;
//如果有右孩子,且 右孩子大于左孩子,将右孩子索引赋值给j
if (j + 1 <= size && queue[j + 1] > queue[j]) {
j = j + 1;
}
//现在 j 保存的是左右孩子中较大的节点的索引
//比较当前节点和左右孩子中较大的节点
//如果比左右孩子中较大的节点还大,则不用向下翻了
if (queue[k] > queue[j]) {
break;
}
//否则交换当前节点和左右孩子中较大的节点
swap(k, j);
//把左右孩子中较大的节点的索引赋值给k,继续向下翻
k = j;
}
}
//交换两个位置
private void swap(int i, int j) {
int t = queue[i];
queue[i] = queue[j];
queue[j] = t;
}
}
下面是测试代码:
public static void main(String[] args) {
QPriorityQueueInt queue = new QPriorityQueueInt();
//随便弄5个数入队,数越大优先级越大
//由于我们的QPriorityQueueInt默认只支持10个元素
//所以插入的节点个数不要多于10个
queue.add(3);
queue.add(5);
queue.add(1);
queue.add(8);
queue.add(7);
//打印
System.out.println(queue.poll());
System.out.println(queue.poll());
System.out.println(queue.poll());
System.out.println(queue.poll());
System.out.println(queue.poll());
}
输出如下:
8
7
5
3
1
从输出可以看出来,虽然7是最后入队的,但是优先级比较高,第二次就打印出来了。 优先级队列,同样是用数组实现。但是入队的效率比单纯的用数组排序要高多了。
至于扩容机制,读者可以自己查阅相关资源,自己实现。